Identity Matrices Expii
Determinants DETERMINANTS Our definition of determinants is as follows. If A = [a] is one by one, then det (A) = a. If A is the 2 by 2 matrix a b c d then det (A) = ad - bc. In the general case, we assume that one already knows how to compute determinants of size smaller than n by n. Let A be an n by n matrix. Then det (A) is defined as

Solved Find the determinate of this 4x4 matrix using
The reduced row echelon form of the matrix is the identity matrix I 2, so its determinant is 1. The second-last step in the row reduction was a row replacement, so the second-final matrix also has determinant 1. The previous step in the row reduction was a row scaling by − 1 / 7; since (the determinant of the second matrix times − 1 / 7) is 1, the determinant of the second matrix must be.

How to Find the Determinant of a 5x5 Matrix YouTube
Since the identity matrix is diagonal with all diagonal entries equal to one, we have: \[\det I=1.\] We would like to use the determinant to decide whether a matrix is invertible. Previously, we computed the inverse of a matrix by applying row operations. Therefore we ask what happens to the determinant when row operations are applied to a matrix.
PPT Chapter 8 Matrices and Determinants PowerPoint Presentation, free download ID2690088
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. The determinant of a matrix A is commonly denoted det (A), det A, or |A|. Its value characterizes some properties of the matrix and the linear map represented by the matrix.
Find a Matrix B Such that A * B is the Identity Matrix and det(A) is not Zero YouTube
Swapping two rows of a matrix does not change | det (A) |. The determinant of the identity matrix I n is equal to 1. The absolute value of the determinant is the only such function: indeed, by this recipe in Section 4.1, if you do some number of row operations on A to obtain a matrix B in row echelon form, then

Determinant of 3x3 Matrices, 2x2 Matrix, Precalculus Video Tutorial YouTube
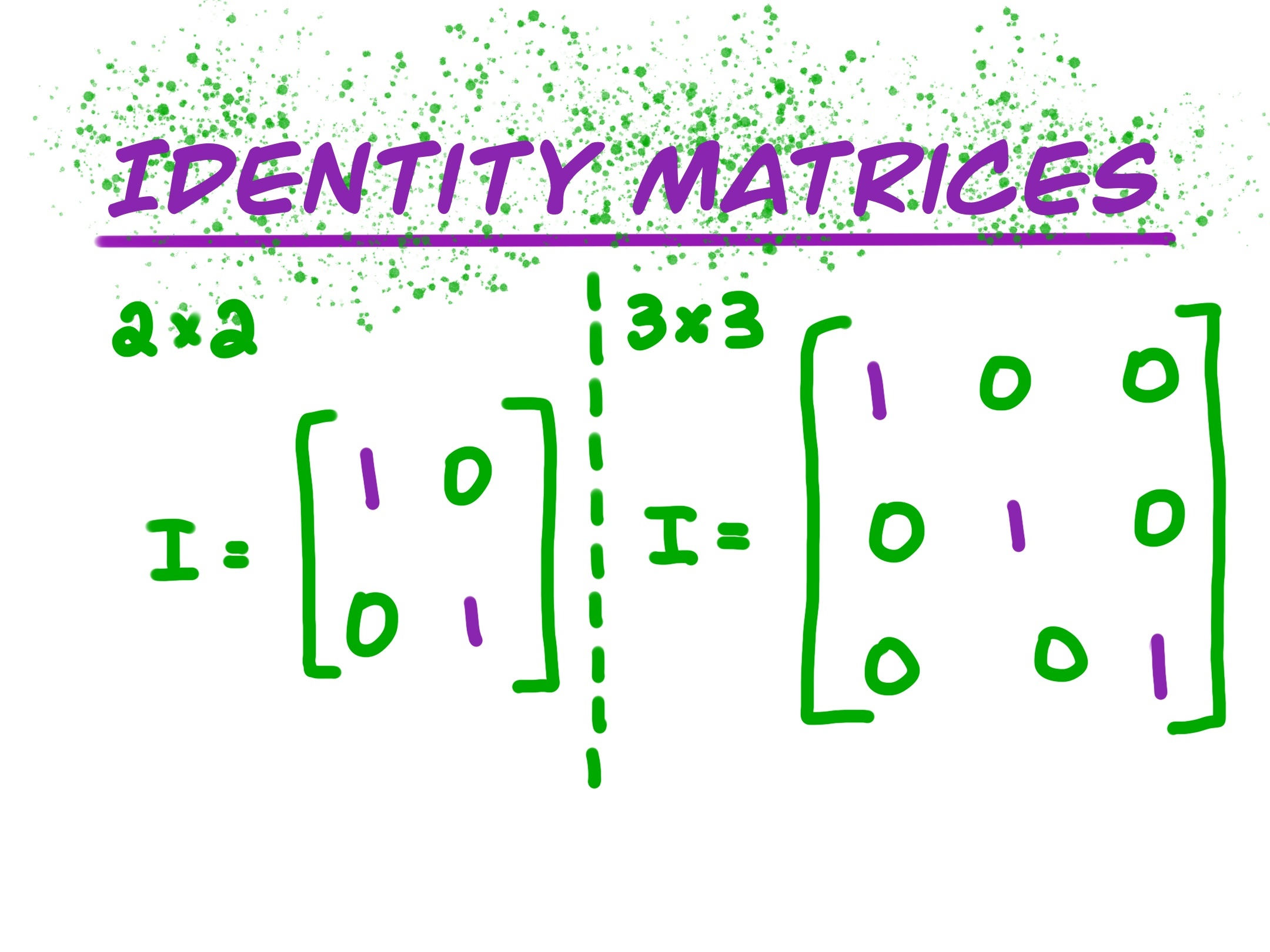
Identity Matrix Definition An identity matrix is a square matrix in which all the elements of principal diagonals are one, and all other elements are zeros. It is denoted by the notation "I n" or simply "I". If any matrix is multiplied with the identity matrix, the result will be given matrix. The elements of the given matrix remain unchanged.
How to Find The Determinant of a 4x4 Matrix (Shortcut Method) YouTube
Determinant of the Identity Matrix proof Asked 7 years, 8 months ago Modified 7 years, 8 months ago Viewed 27k times 2 I have trouble proving that for all n n, det(In) = 1 det ( I n) = 1 In I n is Identity Matrix nxn n x n I tried to use Inductive reasoning but without any progress linear-algebra Share Cite Follow edited Apr 23, 2016 at 13:24

Matrix Determinant Calculator 2x2 Deb Moran's Multiplying Matrices
For matrices with other dimensions you can solve similar problems, but by using methods such as singular value decomposition (SVD). 2. No, you can find eigenvalues for any square matrix. The det != 0 does only apply for the A-λI matrix, if you want to find eigenvectors != the 0-vector.

Solved For the n x n matrix compute det (A + tI) where I is
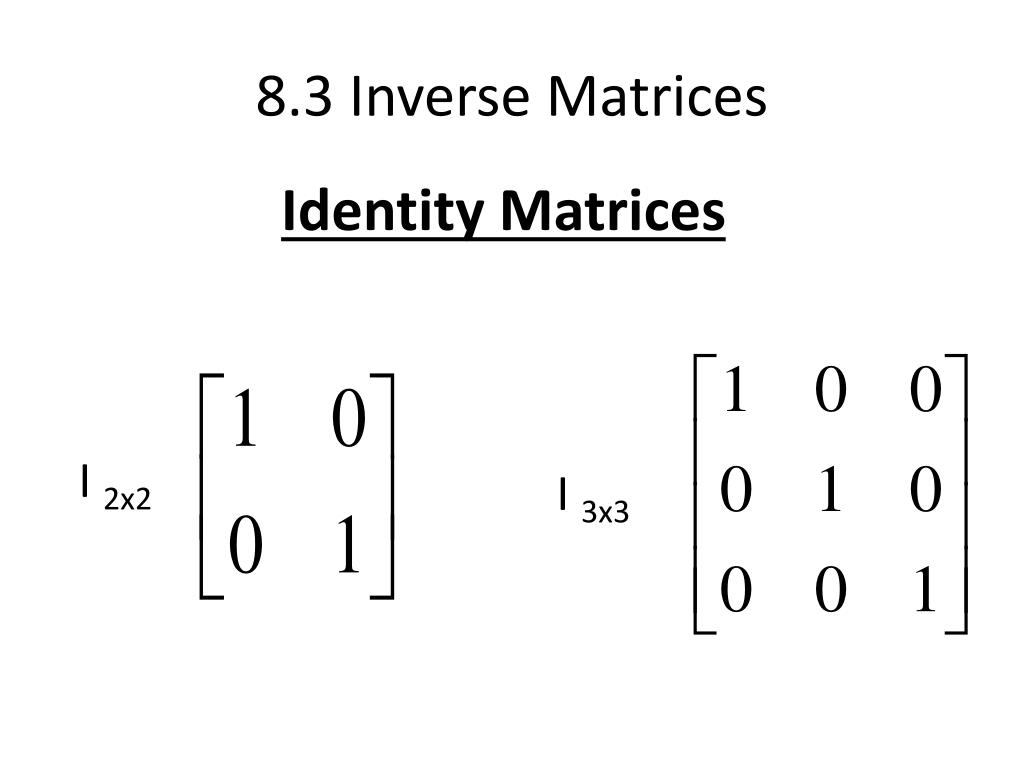
The n × n identity matrix, denoted I n , is a matrix with n rows and n columns. The entries on the diagonal from the upper left to the bottom right are all 1 's, and all other entries are 0 . For example: I 2 = [ 1 0 0 1] I 3 = [ 1 0 0 0 1 0 0 0 1] I 4 = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1]
27.A square matrix of order n is both involuntary and idempotent matrix. The value of the
In the resulting matrix, the \(i\)th row is zero, so \(\det(A) = 0\) by the first part. Still assuming that \(A\) is upper-triangular, now suppose that all of the diagonal entries of \(A\) are nonzero. Then \(A\) can be transformed to the identity matrix by scaling the diagonal entries and then doing row replacements:

Determinant of a matrix cookiegaret
Math 21b: Fact sheet about determinants. matrix A is a scalar, denoted det (A). [Non-square matrices do not have determinants.] The determinant of a square matrix A detects whether A is invertible: If det (A)=0 then A is not invertible (equivalently, the rows of A are linearly dependent; equivalently, the columns of A are linearly dependent.

PPT Matrices Inverse Matrix PowerPoint Presentation, free download ID5601422
1 The determinant of a permutation matrix P is 1 or −1 1 = −1. 0 depending on whether P exchanges an even or odd number of rows. From these three properties we can deduce many others: 4. If two rows of a matrix are equal, its determinant is zero. This is because of property 2, the exchange rule.

PPT Matrix Algebra Basics PowerPoint Presentation, free download ID150371
An Identity Matrix is a square matrix of any order whose principal diagonal elements are all ones and the rest other elements are all zeros. In this lesson, we will look at what identity matrices are, how to find different identity matrices, some properties of identity matrices, and the determinant of an identity matrix.

linear algebra Origin and use of an identity of formal power series \det(1 \psi T) = \exp
Definition 2.6.1 2.6. 1: The Inverse of a Matrix. A square n × n n × n matrix A A is said to have an inverse A−1 A − 1 if and only if. AA−1 = A−1A = In A A − 1 = A − 1 A = I n. In this case, the matrix A A is called invertible. Such a matrix A−1 A − 1 will have the same size as the matrix A A. It is very important to observe.

Identity Matrix
The identity matrix is the only idempotent matrix with non-zero determinant. That is, it is the only matrix such that: When multiplied by itself, the result is itself. All of its rows and columns are linearly independent. The principal square root of an identity matrix is itself, and this is its only positive-definite square root.

How to Evaluate the Determinant of a 3x3 Matrix Quick & Easy Method YouTube
In order for that to happen, they must live in different dimensions. So the number of dimensions of that I matrix is the same as its number of columns. But we already know that number of col = num of rows of the 2nd matrix. Therefore the I matrix would be n*n where n=num of of of the 2nd matrix. •.