
Highly composite numbers
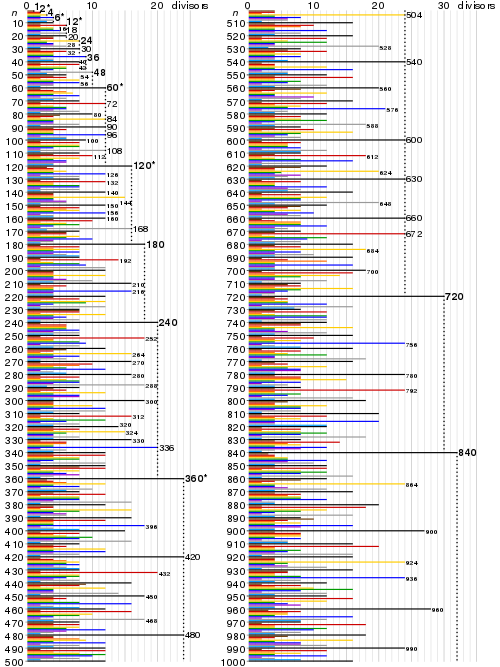
There are an infinite number of highly composite numbers, and the first few are 1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040,. (OEIS A002182 ). The corresponding numbers of divisors are 1, 2, 3, 4, 6, 8, 9, 10, 12, 16, 18, 20, 24, 30, 32,. (OEIS A002183 ).

Transdecimal Observatory Argam Kinoctove
In number theory, a superior highly composite number is a natural number which, in a particular rigorous sense, has many divisors. Particularly, it is defined by a ratio between the number of divisors an integer has and that integer raised to some positive power.

Kinoctoval Geometric Progressions & SCHN Totatives s7836b14
10 Things You Might Not Know About Mativ. Adhesives Films Mativ Brands Nettings Nonwovens Paper Release Liners. SWM and Neenah are now Mativ, a global leader in specialty materials. We're making critical components and solutions to solve our customers' challenges.
Superior highly composite number Alchetron, the free social encyclopedia
A highly composite number is a positive integer with more divisors than any smaller positive integer has. A related concept is that of a largely composite number, a positive integer which has at least as many divisors as any smaller positive integer.

8 Free Prime and Composite Numbers Anchor Chart
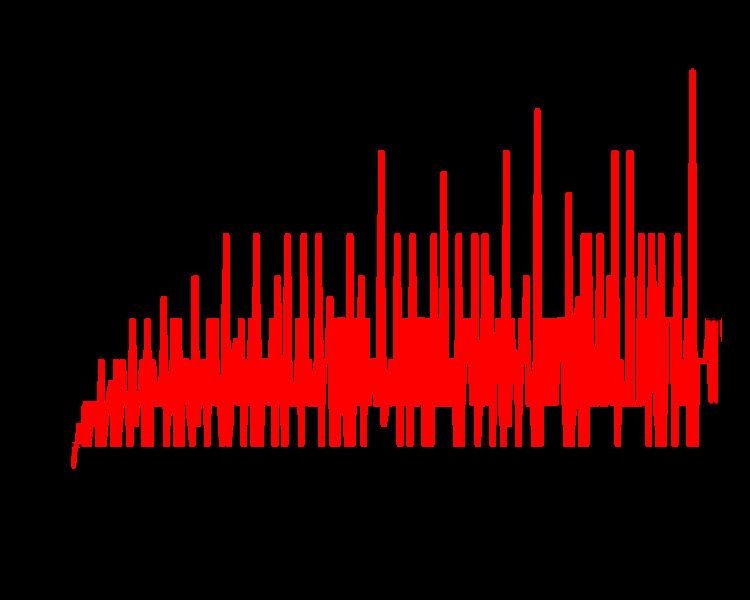
A superior highly composite number is a natural number which has more divisors than any other number scaled relative to the number itself. number-theory elementary-number-theory prime-numbers divisibility divisor-sum Share Cite Follow asked Sep 6, 2014 at 23:22 Omega Force 822 5 14 1
Highly composite numbers
1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040, 7560, 10080, 15120, 20160, 25200, 27720, 45360, 50400, 55440, 83160, 110880, 166320, 221760, 277200, 332640, 498960, 554400, 665280, 720720, 1081080, 1441440, 2162160 ( list ; graph ; refs ; listen ; history ; text ; internal format )

MegaFavNumbers superior highly composite numbers and roundness YouTube
In mathematics, a superior highly composite number is a natural number which, in a particular rigorous sense, has many divisors. Particularly, it's defined by a ratio between the number of divisors an integer has and that integer raised to some positive power.

A superior highly composite number is a natural number which has more divisors than any other
In mathematics, a superior highly composite number is a certain kind of natural number. Formally, a natural number n is called superior highly composite iff there is an ε > 0 such that for all natural numbers k ≥ 1, where d(n), the divisor function, denotes the number of divisors of n. The first few superior highly composite numbers are 2, 6.
Superior highly composite number Detailed Pedia
superior highly composite number. Natural Language; Math Input; Extended Keyboard Examples Upload Random. Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music…

Composite Numbers
A superior highly composite number is a positive integer n for which there is an e>0 such that (d (n))/ (n^e)>= (d (k))/ (k^e) for all k>1, where the function d (n) counts the divisors of n (Ramanujan 1962, pp. 87 and 115).
[Solved] Are all highly composite numbers even? 9to5Science
For s=1, these numbers have been called superabundant by L. Alaoglu and P. Erdős , , and the generalized superior highly composite numbers have been called colossally abundant. The real solution of 2 s +4 s +8 s =3 s +9 s is approximately 1.6741. 10.60. For s=1, the results of this and the following section are in and . 10.62.

Peter Karpov on Twitter "All possible ways of dividing superior highly composite numbers (60
The number twelve, a superior highly composite number, is the smallest number with four non-trivial factors (2, 3, 4, 6), and the smallest to include as factors all four numbers (1 to 4) within the subitizing range, and the smallest abundant number.

Numbers
For a superior highly composite number n there exists a positive real number ε such that for all natural numbers k smaller than n we have. and for all natural numbers k larger than n we have. where d(n), the divisor function, denotes the number of divisors of n.The term was coined by Ramanujan (1915).. The first 15 superior highly composite numbers, 2, 6, 12, 60, 120, 360, 2520, 5040, 55440.

Prime Numbers and Composite Numbers Explained Turito
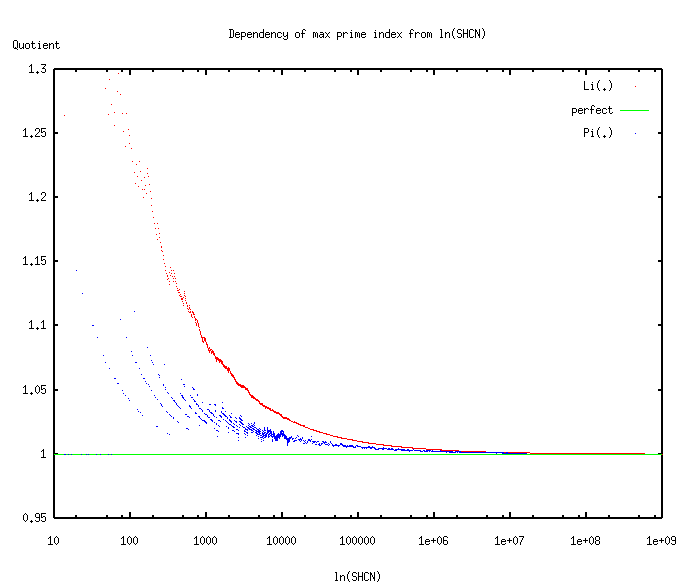
34. The number of divisors of a superior highly composite number. 35. The maximum value of d(N)N1/x for a given value of x. 36. Consecutive superior highly composite numbers. 37. The number of superior highly composite numbers less than a given number. A table of the first 50 superior highly composite numbers. 38.

Prime and composite numbers Education is the most important
A number is superior highly composite whenever it has the largest SHCN score for some positive e - when it can be given some disadvantage with the smaller numbers and still have a higher divisor score. The first highly composite number that fails this is 24. It has 8 divisors, and for any e, 8 / 24 e makes this score smaller than for some.

Superior highly composite number Wikiwand
Superior highly composite numbers: positive integers n for which there is an e > 0 such that d (n)/n^e >= d (k)/k^e for all k > 1, where the function d (n) counts the divisors of n ( A000005 ). (Formerly M1591 N0620) 43